Софья Ковалевская. Доктор философии.

В Берлин Софья Васильевна вернулась лишь поздней осенью, в конце октября 1873 года, в связи с тем, что летом в городе была эпидемия холеры. Занятия с Вейерштрассом продолжались, однако теперь он уделял своей ученице меньше времени, так как был сильно загружен обязанностями ректора.

Математические способности Софьи Васильевны всегда восхищали Вейерштрасса. «Что касается математического образования Ковалевской, то могу заверить, что я имел очень немногих учеников, которые могли бы сравниться с нею по прилежанию, способностям, усердию и увлечению наукой»,— писал он своему товарищу по работе.

За четыре года (из которых часть времени ушла на поездки) Ковалевская не только усвоила курс математического факультета университета, но и написала три работы:
1) К теории уравнений в частных производных;
2) О приведении одного класса абелевых интегралов третьего,ранга к интегралам эллиптическим;
3) Дополнения и замечания к исследованию Лапласа о форме кольца Сатурна.
Каждая из этих работ была бы достаточна для присуждения за неё степени доктора философии.

В 1874 году Геттингенский университет присудил Ковалевской степень доктора философии «с высшей похвалой», причём она была освобождена от обязательных экзаменов, что иногда допускали в случае очень хорошей работы.

Особенно важно первое исследование Ковалевской, так как рассмотренные в нём вопросы имеют широкое применение в различных задачах механики и физики. Крупный французский математик Коши рассматривал ещё ранее Ковалевской аналогичные вопросы, но в применении к более простым уравнениям. Кроме того, Ковалевская обнаружила некоторые особые случаи, существования которых математики того времени не подозревали. Теореме, высказанной Коши, Ковалевская дала окончательную и более общую форму, поэтому принято называть эту теорему теоремой Коши-Ковалевской.

Геометрический принцип интегрирования

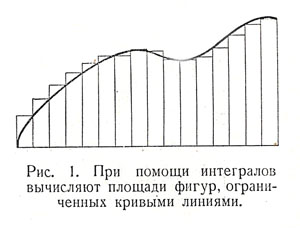
Вторая задача потребовала от Ковалевской глубокого знания сложной математической теории интегралов Абеля. Интегралом называется предел, к которому стремится сумма бесконечно большого числа бесконечно малых сла гаемых. При помощи интегралов вычисляются площади фигур, ограниченных кривыми линиями. Разбивая фигуру на узкие полосы, заменяя площадь каждой полосы площадью прямоугольника и складывая эти площади, находят приближённую величину площади. Чем больше полос и'чем меньше площадь каждой полосы, тем точнее результат. Абсолютно точное значение площади получается при сложении бесконечно большего числа бесконечно узких полос. При помощи интегралов вычисляются также объёмы, длины дуг и т. д.

В зависимости от того, какая кривая ограничивает искомую площадь, интеграл, её выражающий, может быть более или менее сложным. Во многих случаях получаются абелевы интегралы, которые относятся к упомянутым выше функциям Абеля. Различают абелевы интегралы первого, второго, третьего и т. д. рангов в порядке возрастающей сложности их. Вопрос о возможном упрощении абелевых интегралов второго ранга был предложен Вейерштрассом его ученику Кенигсбергеру, лекции которого слушала Ковалевская в 1869 году. Аналогичную задачу, но более сложную — для интегралов третьего ранга — решила Софья Васильевна.

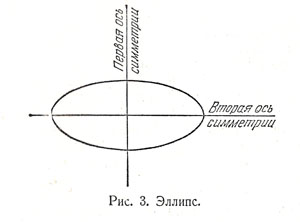
Третья работа Ковалевской относится к вопросу о форме кольца Сатурна. Как известно, планета Сатурн опоясана кольцом, которое имеет вид тора (баранки). Но каково поперечное сечение кольца? Является ли оно кругом или ограничено некоторой сплюснутой кривой? Великий французский математик и астроном Лаплас решил эту задачу в очень упрошенном виде. Предположив, что кольцо Сатурна слагается из нескольких тонких колец, и исходя из этой предпосылки, Лаплас нашёл, что поперечное сечение кольца Сатурна ограничено кривой, которая называется эллипсом — она представляет собою-сплюснутую окружность, симметричную относительно двух взаимно перпендикулярных осей.

Эллипс

Овал

В то время среди математиков начал проявляться интерес к вопросам устойчивости движения. Всем известно, по когда волчок движется, быстро вращаясь, то даже довольно сильный удар по нему лишь на время отклоняет его, а затем происходит восстановление первоначального движения. Форма движения, при которой малые, вызываемые извне отклонения, или, как говорят, возмущения, с течением времени сглаживаются, так что тело восстанавливает первоначальное движение, называется устойчивой формой. В том же случае, когда малое начальное отклонение с течением времени возрастает, говорят, что движение неустойчиво.

Устойчивое (а) и неустойчивое (б) положение маятника

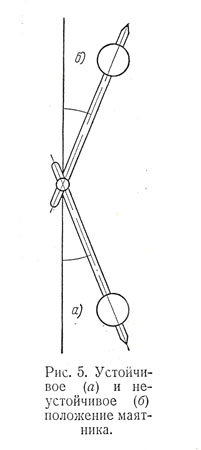
Частным случаем устойчивости движения является устойчивость равновесия, которую можно пояснить на простом примере маятника (рис. 5) . Нижнее положение маятника, т. е. такое, при котором центр его тяжести находится ниже точки подвеса, устойчиво, так как если мы выведем маятник из положения 5, а, то он будет возвращаться к нему. Верхнее же положение, при котором центр тяжести выше точки опоры, неустойчиво — маятник будет легко отклоняться от этого положения.

Большой познавательный интерес представляет задача об устойчивости фигур небесных тел, которые в некоторой стадии своего существования могут состоять из расплавленной жидкой массы. Возникает вопрос: какие формы может принимать жидкая масса, вращающаяся равномерно с постоянной угловой скоростью?

Трёхосный эллипсоид

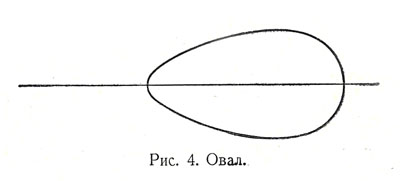
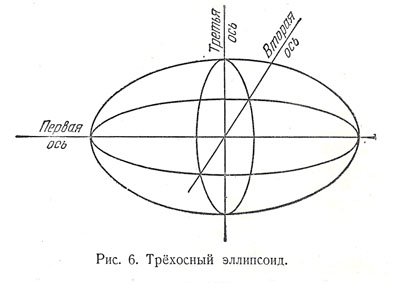
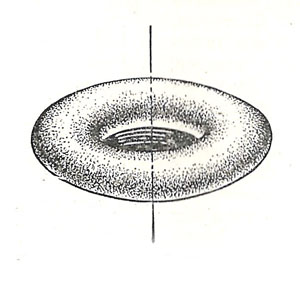
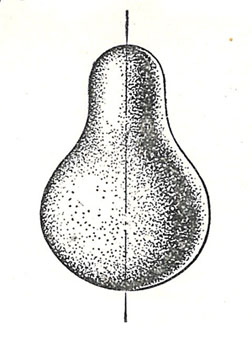
Найдено, что одной из таких форм является трёхосный эллипсоид, вращающийся вокруг малой оси. Жидкая масса может принимать также форму торообразных и грушевидных тел, вращающихся вокруг оси.

Торообразное тело

Грушевидное тело

Однако в действительности среди небесных тел грушевидные и торообразные не наблюдаются (исключением является кольцо Сатурна, о котором будет сказано ниже). Чтобы понять, почему так происходит, нужно познакомиться с важным свойством вращающейся жидкости — с устойчивостью её формы. Если частицы жидкости после деформации (изменения формы тела) возвращаются к своему первоначальному состоянию, то такая формa устойчива. Если же деформация со временем увеличивается, пока тело не распадётся, то мы имеем дело с неустойчивой формой. Исследования крупнейших математиков: русского, Александра Михайловича Ляпунова, и французского, Анри Пуанкаре, показали, что трёхосный эллипсоид будет устойчивым или неустойчивым в зависимости от соотношений между его размерами, массой и угловой скоростью вращения (при очень большой скорости невозможны не только устойчивость, но и равновесие).

Грушевидные формы, как показал Ляпунов, неустойчивы (т. е. они могут существовать, если не будут испытывать никаких внешних воздействий, но малейшие «возмущения» приводят к их разрушению). Этим и объясняется то, что среди небесных тел не обнаружены тела грушевидной формы. Что же касается торообразных тел, то они были исследованы С. В. Ковалевской. Она показала, что такие тела при некоторых формах поперечного сечения их могут образовываться вращающейся жидкостью. Её интересовал также и вопрос о том, устойчивы ли торообразные тела. Однако она занималась им мало, так как к тому времени учёные установили, что кольцо Сатурна состоит из отдельных твёрдых тел, и, следовательно, не является жидкостью.

Уже после смерти Ковалевской другими учёными было обнаружено, что кольцевидное жидкое тело не может быть устойчивым, т. е. оно может существовать лищь при отсутствии каких бы то ни было внешних влияний, в противном же случае неизбежно должно распасться. Таким образом, вопрос о кольцевидной форме небесного тела в настоящее время исчерпан до конца (так же, как вопрос о грушевидных формах), и известная доля заслуги здесь принадлежит Ковалевской.

П.Я.Полубояринова-Кочина. «Софья Ковалевская. Её жизнь и деятельность».

Далее: Материнство и банкротство

Главная   |  Биографии учёных  |  Ковалевская Софья Васильевна  |  Доктор философии