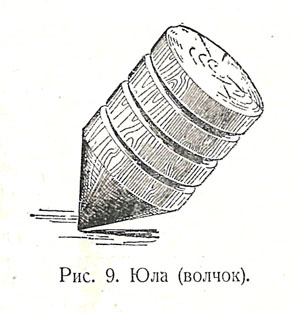
Софья Ковалевская. Задача о вращении твёрдого тела

Самую большую славу Ковалевской принесла задача о вращении тяжёлого твёрдого тела вокруг неподвижной точки. Пояснить сущность этой задачи можно на примере волчка или юлы. В старину была распространена детская игрушка юла, которую делали из обрубка дерева, обточенного так, чтобы получилось соединение конуса с цилиндром. На цилиндрическую часть наматывали верёвку. Если быстро дёрнуть за верёвку и тотчас спустить юлу на землю, то она, вращаясь вокруг своей оси, начнёт перемещаться, причём остриё юлы будет описывать некоторую кривую.

Юла (волчок)

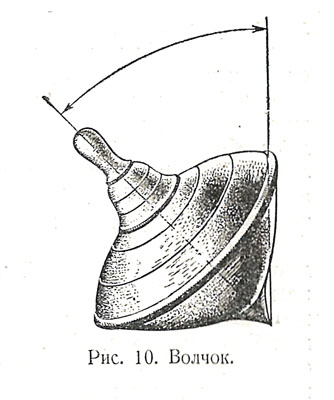
Современный волчок представляет красивую металлическую игрушку с более совершенным способом запуска, однако сущность остаётся здесь той же самой: нужно привести волчок во вращение, после чего он будет двигаться более или менее долго в зависимости от величины силы трения острия о поверхность, по которой оно перемещается.

Волчок

Движение волчка обладает рядом замечательных свойств. Если ударить движущийся волчок, причём направление удара будет известно, то можно точно указать, в какую сторону наклонится ось волчка. Это отклонение будет кратковременным; волчок быстро возвратится в первоначальное положение. Такое свойство, как мы уже говорили раньше, называется устойчивостью движения волчка.

По принципу волчка устроен прибор, называемый гироскопом. Слово «гироскоп» происходит от соединения греческих слов «кружусь» и «наблюдаю» и, следовательно, :означает прибор для наблюдения вращения. Гироскопические приборы имеют широкое применение в современной технике. Они служат для определения курса самолётов, судов и т. д., для стабилизации их движения (т. е. для того, чтобы сделать это движение устойчивым), а также для других целей.

Гироскоп Н. И. Мерцалова

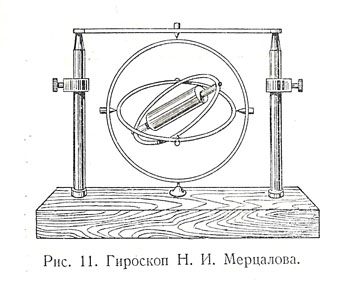
Ковалевская занялась изучением общих свойств гироскопа и характера его движения. Профессор механики Николай Иванович Мерцалов сконструировал прибор, на котором можно пояснить задачу Ковалевской. Он состоит из довольно узкого цилиндра с двумя тонкими кольцами, неподвижно с ним связанными,— такая форма позволяет уменьшить сопротивление воздуха при движении. Два других кольца позволяют цилиндру свободно вращаться вокруг двух осей — вертикальной и горизонтальной.

Траектории движения точки на гироскопе

Одну точку на цилиндре Мерцалов сделал светящейся. Гироскоп был приведён в движение в темноте, перед открытым объективом фотоаппарата. Светящаяся точка запечатлелась на снимке в виде очень сложной кривой. На рисунке выше приведены такие кривые, полученные при разных начальных положениях оси цилиндра и различных скоростях вращения. Вот как сложен путь отдельной точки гироскопа!

Математическая задача, которую решала Ковалевская, состояла в том, чтобы рассчитать этот путь и найти положение заданной точки в любой момент времени. Полное решение такой задачи для гироскопа произвольной формы и положения встречает большие трудности. Поэтому для решения задачи прибегают к отдельным частным случаям.

Варианты задачи о вращении твердого тела. Иллюстрация Н.Е.Жуковского

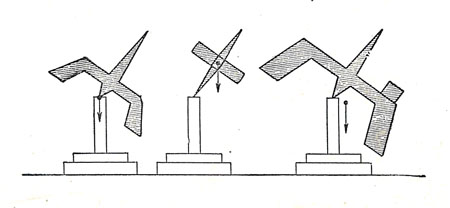
На рисунке, сделанном Н.Е.Жуковским для пояснения результатов, полученных Ковалевской, представлены три таких частных случая. Два первых были известны до Ковалевской, третий исследован ею. В первом случае гироскоп представляет тело произвольной формы, опирающееся на подставку таким образом, что точка опоры совпадает с центром тяжести тела. Этот случай был рассмотрен великим математиком, петербургским академиком Эйлером.

Второй гироскоп представляет тело вращения, т. е. тело, получаемое вращением некоторой линии вокруг прямой, которая называется осью симметрии; при этом центр тяжести его находится в одной из точек этой оси, не совпадая с точкой опоры. Такое тело, конечно, упадёт, если мы поставим его так, как указано на рисунке, и не сообщим ему вращательного движения. Однако вращающееся тело может в некоторый момент времени занимать указанное положение, меняя его в последующие моменты. Этот случай был рассмотрен знаменитым французским математиком Лагранжем.

На этих двух случаях дело остановилось, так как изучение других случаев было необычайно сложным. Ковалевская произвела глубокий анализ задачи, выяснила возможности решения её современными математическими методами и открыла новый, прославивший её случай, когда решение задачи можно полностью провести и довести до конца.

Случай, открытый Ковалевской, Н. Е. Жуковский изобразил в виде третьего волчка. Этот волчок не вполне симметричен; его центр тяжести не лежит на оси симметрии, а смещён относительно точки опоры.

Ковалевская полностью решила задачу для этого частного случая, причём решение получилось гораздо более сложным, чем в первых двух случаях. Таким образом, Ковалевская поставила своё имя рядом с именами Эйлера и Лагранжа, завершив исследования, относящиеся к классической задаче о вращении твёрдого тела. Ей понадобилось при этом глубокое знакомство с очень сложным разделом математикигиперэллиптическими функциями, относящимися к абелевым функциям, о которых мы упоминали выше.

П.Я.Полубояринова-Кочина. «Софья Ковалевская. Её жизнь и деятельность».

Далее: Премия Парижской Академии наук

Главная   |  Биографии учёных  |  Ковалевская Софья Васильевна  |  Задача о вращении твёрдого тела